백트래킹 문제

 

<15649번 : N과 M(1)>

import sys
input = sys.stdin.readline

def backtracking() :
    # 원하는 길이의 순열이 완성되면 출력
    if len(array) == m:
        print(" ".join(map(str, array))) # 리스트의 원소를 공백으로 구분된 문자열로 변환 후 출력
        return
    # i는 1부터 N까지의 숫자
    for i in range(1, n+1):
        # 순열이므로 겹치는지 아닌지 확인
        # 중복이 아니면 숫자 i를 리스트에 추가
        if i not in array:
            array.append(i)
            backtracking()
            # return 되어서 돌아오면 전 단계로 돌아감
            # 예를 들어 순열이 1,2,3이면 return 되어서 돌아온 후 3이 pop되고
            # 1,2에서 다음 값을 찾는 형식으로 전 단계로 돌아가는 것
            array.pop()

n,m = map(int, input().split())
array=[]
backtracking()

 

☆ 백트래킹은 '완전탐색(Brute Force)'을 하면서 조건을 만족하지 않으면 탐색을 중단하는 방식

 

☆ for문 설명

- 1부터 N까지의 숫자를 반복문을 통해 확인

- 만약 숫자 i가 array 리스트에 존재하지 않는다면(if i not in array), i를 추가

- 이후, backtracking()을 재귀적으로 호출하여 다음 숫자를 선택

- 재귀 호출이 끝난 후에는 pop()을 사용하여 마지막으로 추가한 숫자를 제거하여, 원래 상태로 되돌린다.

 

 

▽ 백트래킹을 사용한 이유

1. 모든 경우의 수를 탐색하면서도, 불필요한 탐색은 하지 않음 → 중복을 방지하기 위해 'if i not in array:'로 이미 사용된 숫자는 선택하지 않음

2. DFS(깊이 우선 탐색)방식으로 해결 가능 → 한 번 선택한 숫자는 다음 재귀 호출에서 사용되지 않도록 조절하여 모든 경우를 탐색함

3. 재귀를 이용해 자연스럽게 수열을 생성하고, 백트래킹으로 돌아갈 수 있음 → array.pop()을 사용하여 이전 상태로 되돌아가면서 새로운 조합을 탐색함

 

▽ 시간 복잡도

- 백트래킹을 이용한 순열 생성 알고리즘 → 시간 복잡도는 O(N!)

 

▽ set을 사용하여 중복 확인한 최적화된 코드 → 시간 복잡도 O(1)

import sys
input = sys.stdin.readline

def backtracking():
    if len(array) == m:
        print(" ".join(map(str, array)))
        return

    for i in range(1, n + 1):
        if i not in used:  # ✅ set을 이용한 중복 검사 (O(1))
            array.append(i)
            used.add(i)  # ✅ set에 추가
            backtracking()
            array.pop()
            used.remove(i)  # ✅ set에서 제거 (백트래킹)

n, m = map(int, input().split())
array = []
used = set()  # ✅ 중복 확인을 위한 set
backtracking()

 

 

풀이

https://velog.io/@yusuk6185/%EB%B0%B1%EC%A4%80-15649-N%EA%B3%BC-M-1-%ED%8C%8C%EC%9D%B4%EC%8D%AC-with-%EB%B0%B1%ED%8A%B8%EB%9E%98%ED%82%B9

[백준 15649] N과 M (1) - 파이썬 with 백트래킹

 

 

<15650번 : N과 M(2)>

n,m = list(map(int, input().split()))
s = []
def f(start):
    if len(s) == m:
        print(' '.join(map(str,s)))
        return
    for i in range(start, n+1):
        if i not in s:
            s.append(i)
            f(i+1)
            s.pop()
f(1)

 

- start인자 추가 : start 변수를 사용하여 재귀 호출 시 다음에 선택할 수 있는 숫자의 범위를 제한한다. 이렇게 하면 오름차순을 유지하면서 수열 생성 가능

 

 

<15651번 : N과 M(3)>

 

import sys
input = sys.stdin.readline

def backtracking() :
    if len(arr) == m:
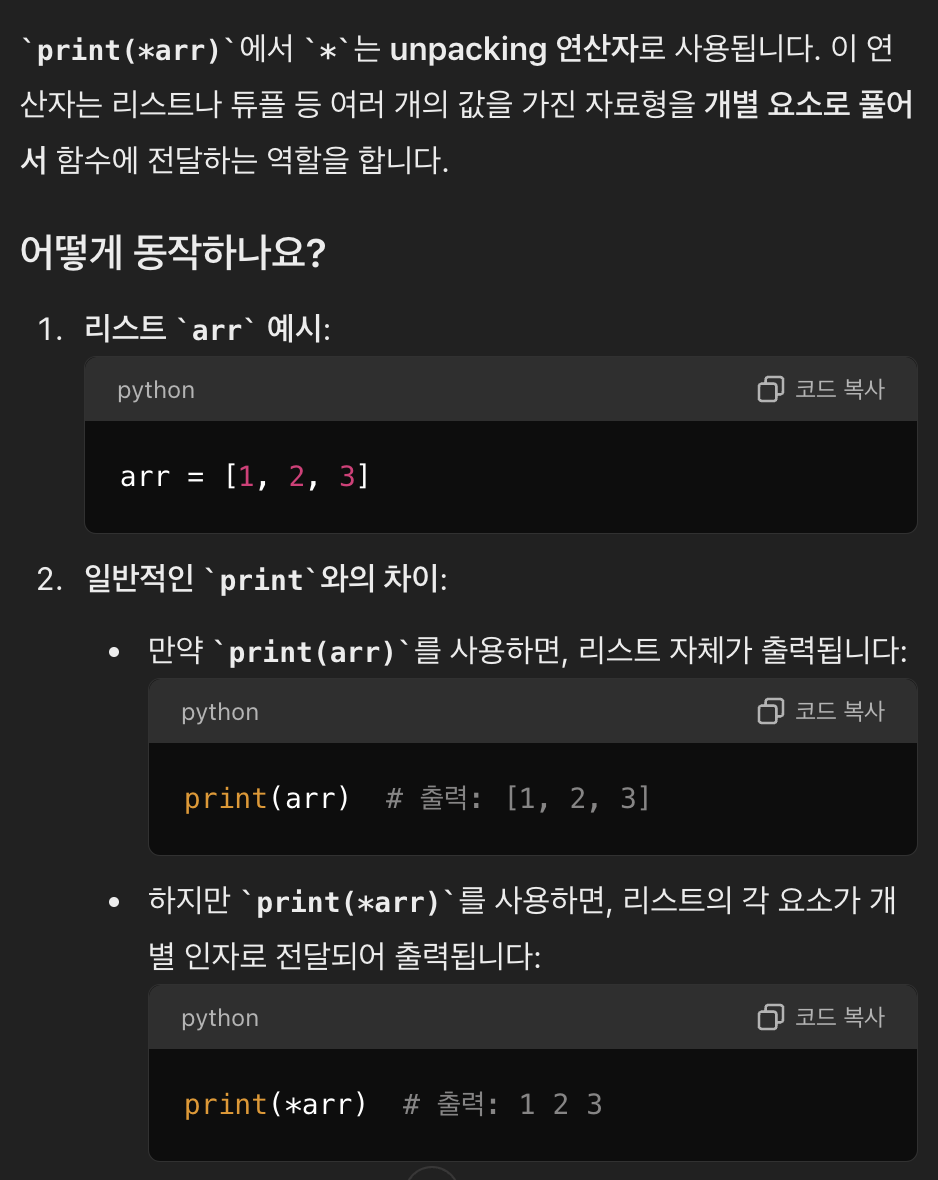
        print(*arr)
        return
    for i in range(1,n+1):
        arr.append(i)
        backtracking()
        arr.pop()

n,m = map(int, input().split())
arr=[]
backtracking()

 

- 15649번과 동일하지만 중복을 허용하기 때문에, for문에서 중복을 확인하는 if문이 삭제됨

 

[다른 풀이]

n, m = map(int, input().split())
s = []
def dfs():
    if len(s) == m:
        print(' '.join(map(str,s)))
        return

    for i in range(1,n+1):
        s.append(i)
        dfs()
        s.pop()
dfs()

 

 

 

<15652번 : N과 M(4)>

 

 

import sys
input = sys.stdin.readline
# 비내림차순..
def backtracking(x) : # 앞의 숫자와 비교해야하므로 파라미터로 넘겨줌
    if len(arr) == m: # array의 길이가 m과 같으면 답 출력
        print(*arr)
        return
    for i in range(x,n+1): # 파라미터로 받은 숫자보다 같거나 커야함
        arr.append(i) # 수를 더해주고
        backtracking(i) # 더한 수를 파라미터로 가지고 backtracking
        arr.pop() # 원 상태로 돌리기 위해 pop

n,m = map(int, input().split())
arr=[]
backtracking()

 

 

- 비내림차순은 같을 때를 포함하는 개념. 오름차순은 확실히 다음 항이 더 커야한다.

- 현재 함수에서는 for문에서 넣은 숫자보다 같거나 커야한다. 파라미터로 넘겨주어서 체크해준다.

- 파라미터로 받은 숫자보다 같거나 커야하기 때문에 x이상 n이하

- 수를 더해주고 더한 수를 파라미터로 가지고 함수 호출

- 원상태로 돌리기 위해 pop

 

[다른 풀이]

n,m = list(map(int,input().split()))
s = []
def f(start):
    if len(s) == m:
        print(' '.join(map(str,s)))
        return
    for i in range(start,n+1):
        s.append(i)
        f(i) # 그냥 오름차순 문제랑 이 부분이 다름!
        s.pop()
f(1)

 

 

<14888번 : 연산자 끼워넣기>

N = int(input())
lst = list(map(int, input().split()))
operators = list(map(int, input().split()))

mx = -1e9
mn = 1e9

def dfs(n, temp):
    global mx, mn

    # 종료 조건
    if n == N-1:
        mx = max(temp, mx)
        mn = min(temp, mn)
        return
    # 하부함수 호출
    if operators[0] != 0: # 덧셈하는 경우
        operators[0] -= 1
        dfs(n+1, temp + lst[n+1])
        operators[0] += 1
    if operators[1] != 0: # 밸셈하는 경우
        operators[1] -= 1
        dfs(n+1, temp - lst[n+1])
        operators[1] += 1
    if operators[2] != 0: # 곱셈하는 경우
        operators[2] -= 1
        dfs(n+1, temp * lst[n+1])
        operators[2] += 1
    if operators[3] != 0: # 나눗셈하는 경우
        operators[3] -= 1
        dfs(n + 1, int(temp/lst[n+1]))
        operators[3] += 1

dfs(0, lst[0])
print(mx)
print(mn)

 

 

- 이 문제는 연산자의 우선순위가 반영되지 않고 순서대로 연산되기 때문에 백트래킹을 사용할 수 있다.

- 출력 범위가 주어졌으므로 범위를 꼭 지정해 줘야함

- 1e9 = 1*109 = 1000000000,

2e9 = 2*109 = 2000000000

- 문제에서 음수를 양수로 나눌 때는 양수로 바꾼 뒤 몫을 취하고, 그 몫을 음수로 바꾼다. → 파이썬의 int()가 해줌!!

* 파이썬은 우리가 기존에 알던 계산법과 음수 나눗셈 연산을 다르게 한다. 몫 연산시, 음수쪽으로 값을 내리기 때문에 더 작은 수가 나오게 된다.

- 잘 정리된 블로그

https://velog.io/@miiingirok/%EB%B0%B1%EC%A4%80-14888.-%EC%97%B0%EC%82%B0%EC%9E%90-%EB%81%BC%EC%9B%8C%EB%84%A3%EA%B8%B0-Python

[BOJ] #14888. 연산자 끼워넣기 (Python)